Pure Matching Models
The Comparative Statics of Sorting with Axel Anderson
In the marriage model, Becker (1973) found that positive (or negative) sorting is efficient with supermodular (or submodular) match payoffs. But characterizing the optimal matching with general production remains unsolved decades later.
Rather than tackle this difficult open problem, we instead ask when match sorting optimally increases. To do this, we first argue that the positive quadrant dependence (PQD) stochastic order on bivariate cdf’s captures an economically meaningful notion of increasing sorting — e.g. a higher correlation of partners.
Our theory turns on synergy: the local cross partial difference or derivative. A natural guess fails: increasing synergies need not raise sorting. But sorting rises if (1) synergy either everywhere increases or proportionately upcrosses through zero, and (2) cross-sectionally, synergy is upcrossing or downcrossing in types.
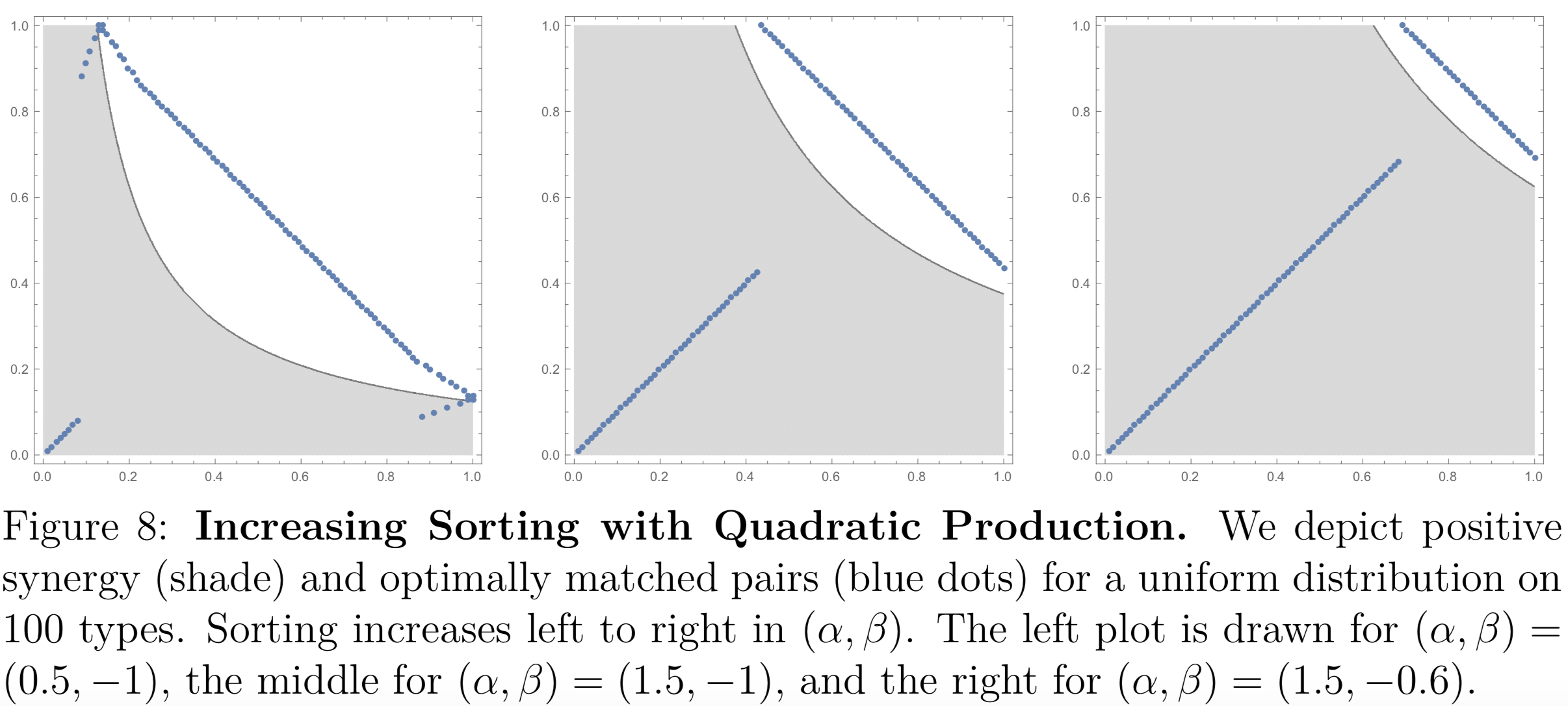
Our proof develops and exploits new monotone comparative statics methods. It proceeds by induction with finitely many types, and secures the continuum type results by taking limits. Our main results are easy to apply. We illustrate all theorems, applying them to the major post 1990 marriage model papers.
To see the nontriviality of our model, consider this example:

For but one of many example, assume quadratic production: φ(x,y) = αxy+β(xy)^2
Matching Models with Search Frictions
Cross-Sectional Dynamics in a Two-Sided Matching Model (1992)
The Marriage Model with Search Frictions (JPE, 2006)
Assortative Matching and Search, Shimer and Smith (Econometrica, 2000)
A Model of Exchange where Beauty is in the Eye of the Beholder (1994 mimeo)
Nonstationary Search, Shimer and Smith (unpublished mimeo 2001)
Frictional Matching Models, Annals Reviews of Economics
Sorting Through Search and Matching Models in Economics,Chade, Eeckhout, and Smith, Journal of Economic Literature, 2017, 55(2), 1–52
Pure Search Theory
My work includes the first characterizations of (1) optimal static (simultaneous) search for heterogeneous options, (2) optimal search for multiple homogenous units, and (3) optimal search with selection effects (hidden and observed components)
- Simultaneous Search with Hector Chade (Econometrica, 5-2006)
- Search at the Margin [= The Theory of MultiUnit Search] with Tono Carrasco (forthcoming American Economic Review, 2017)
- Optimal Sequential Search with Michael Choi
En route to writing the last paper, Michael and I wanted to understand when quasi-concavity was preserved under integration. We resolved that, and a larger class of ordinal aggregation results starting with the single crossing property, by realizing the genius of a classic math result of Samuel Karlin:
Ordinal aggregation results via Karlin’s variation diminishing property, Choi and Smith (Journal of Economic Theory, 2016)
We show that the weighted sum of quasiconcave functions is quasiconcave when the (absolute) decreasing part of every function in the sum grows proportionately faster than the increasing part of every function. Here, f grows proportionately faster than g if g is more risk averse than f, in the Arrow-Pratt sense.
Note: Our working paper Ordinal Aggregation Results via Karlin’s Variation Diminishing Property corrects some typos in the published version.
Matching with Information Frictions
“The Economics of Counterfeiting“, Quercioli and Smith(Econometrica, 2015)
“Student Portfolios and the College Admissions Problem”, Chade, Lewis and Smith (Review of Economic Studies, 2014)
“Dynamic Matching and Evolving Reputations“,Anderson and Smith (Review of Economic Studies, 2010)
Contagious Matching Games, Elena Quercioli and Lones Smith, 2006 Presentation at Penn Search and Matching Conference (December 6, 2006)
