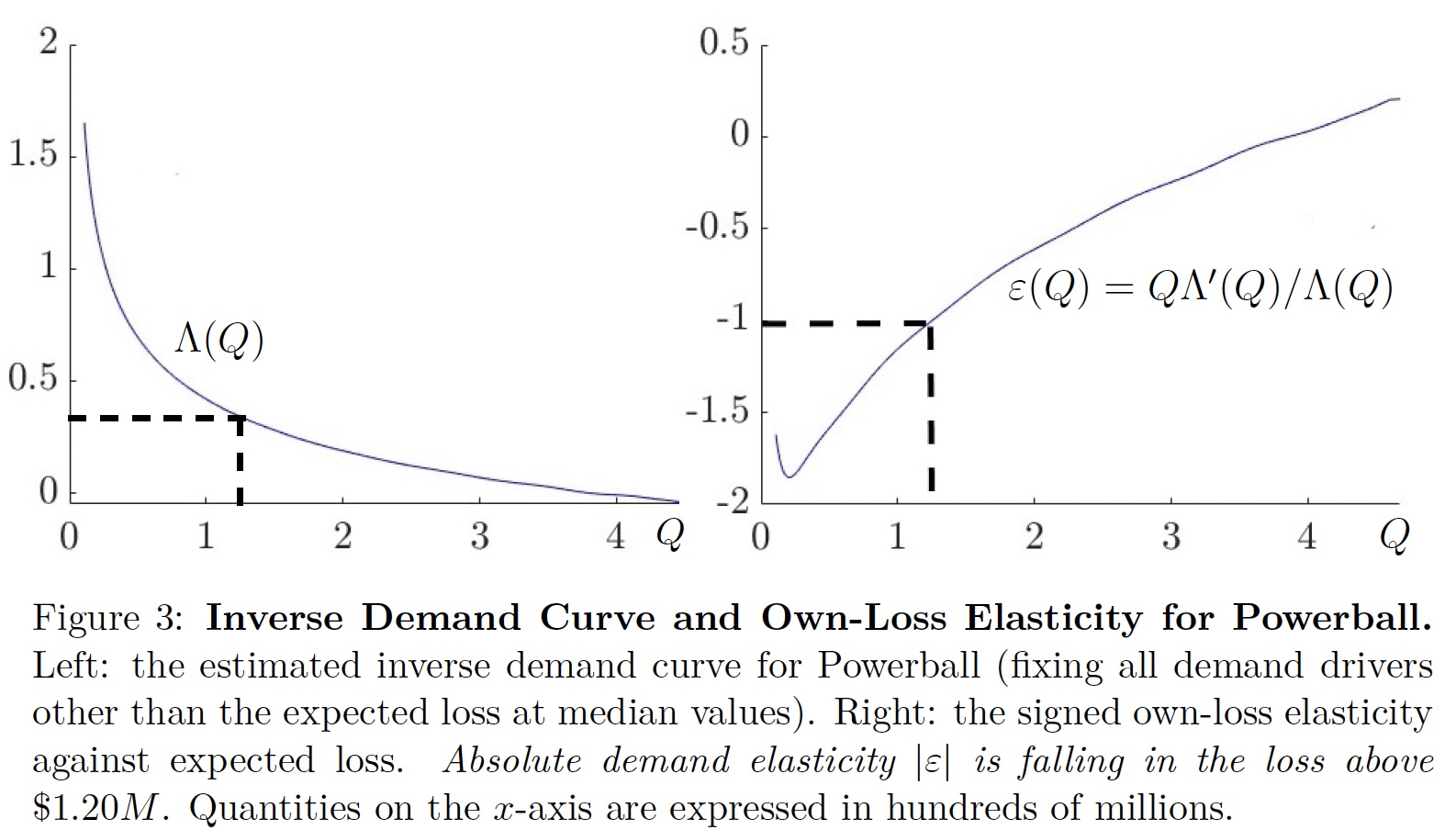
An Equilibrium Model of Rollover Lotteries (with Giovanni Compiani and Lorenzo Magnolfi)
Abstract: We develop a novel model of rollover lottery ticket sales with preferences over thrill and money won. Treating the monetary loss on tickets as an implicit price, lottery rules imply a loss supply curve. Growing jackpots shift the inverse supply down, and help identify the falling demand curve arising from thrill heterogeneity. We non-parametrically estimate the demand for Powerball.
Our model allows risk aversion or risk-loving utility, but slight deviations from risk neutrality are inconsistent with the data. This is a very high stakes empirical test of Rabin’s (2000) calibration thought experiments that low stakes risk aversion yields implausible larger stakes implications. While ticket buyers are risk neutral, Powerball acts a risk loving gambler for rollovers up to $600M. But we prove that Powerball should cap the jackpot at $910 million.
Aside from the model fit, we check risk neutrality in two ways. First, we characterize how log ticket sales should convexly grow in the log jackpot at least up to $408M — which we verify in Powerball data. Next, lottery odds should scale linearly in the population — which we verify in a regression across forty state rollover lotteries.