“Search at the Margin” with Tono Carrasco (American Economic Review, 2017)
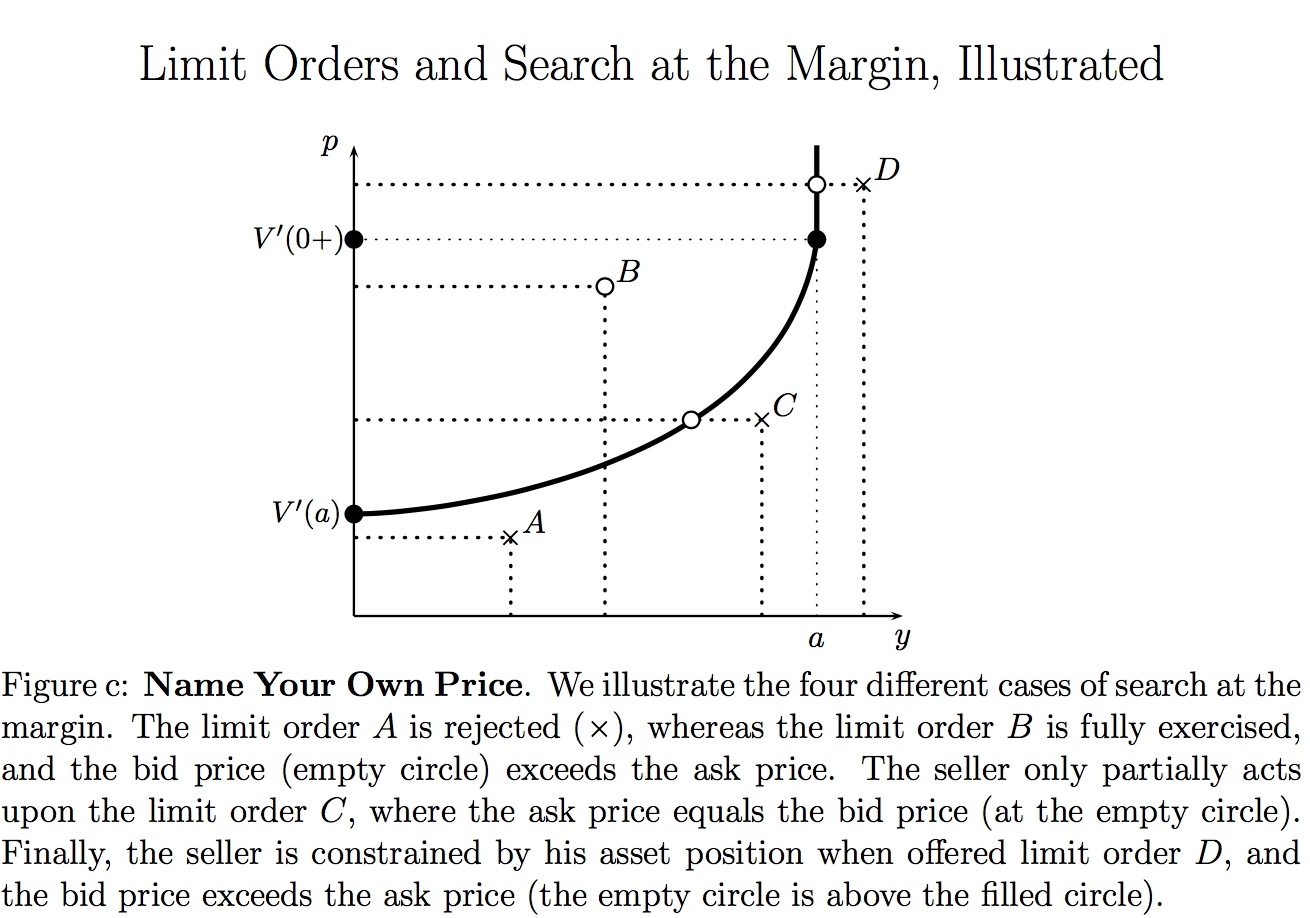
Dynamic models of search theory have thus far confined themselves to single unit search — searching for a lowest priced good or the best wage. While job search is justifiably for a single job, unit search for trades is rather restrictive and unrealistic. The reason is that the dynamic programming problem has proved too formidable. We formulate and solve parallel dynamic programming models extending search theory to (1) multiple indivisible units and (2) perfectly divisible assets. Buyers arrive seeking randomly many units at a random price in (1), or with a random limit order in (2). The seller can partially exercise orders — hence, search at the margin. This problem arises, say, if an airline seeks to sell seats on any given flight using Priceline: buyers arrive periodically, and the airline adjusts its reservation price depending on the number of requested seats, the number of remaining seats, and the time horizon.
The optimal selling strategy adjusts as the asset position falls, reflecting the endogenous holding costs: i.e. the opportunity cost of delaying optionality for the inframarginal units. This depresses reservation prices at the margin. For instance, model (1) subsumes the wage search model, but we inductively argue that the seller is willing to accept less and less money for each additional unit he sells.
While we use induction for the indivisible units model (1), our analysis of continuously divisible assets in (2) exploits recursion and contraction methods. We prove that the Bellman value function is differentiable, and is firstly increasing and strictly concave, and possesses a convex marginal value. Thus, the seller takes greater advantage of more generous offers, and his marginal value shifts up as he unwinds his position, making him less willing to trade. Next, with a falling purchase cap density, the marginal value is strictly convex, and so the seller’s supply response is less elastic at higher prices.
Our model is readily amenable to price-quantity bargaining. We show that greater buyer bargaining power has the same effect as greater search frictions.
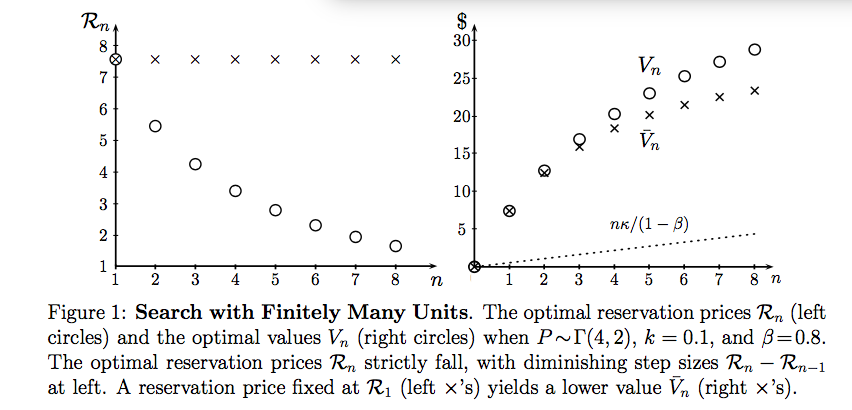
Reservation Prices Fall with the Asset Position
 PS “You miss 100% of the shots you don’t take”. – Wayne Gretzky (greatest hockey player)
PS “You miss 100% of the shots you don’t take”. – Wayne Gretzky (greatest hockey player)
What the quote misses is the option value of not firing shots!
