Rushes in Large Timing Games, Anderson, Smith, and Park (Econometrica, 2017)
It is often said that the early bird gets the worm, and while it sometimes helps to edge out others in in the pursuit of a prize, there are generally limits to going earlier and earlier. This paper introduces and explores a new continuum player timing game in which payoffs depend on timing and your timing rank. Our model subsumes standard wars of attrition and pre-emption games as special cases. Payoffs are continuous and single-peaked functions of the stopping time (peaking at a “harvest time”) and stopping quantile. We show that if payoffs are hump-shaped in the quantile, then a sudden “rush” of players stops in any Nash or subgame perfect equilibrium.
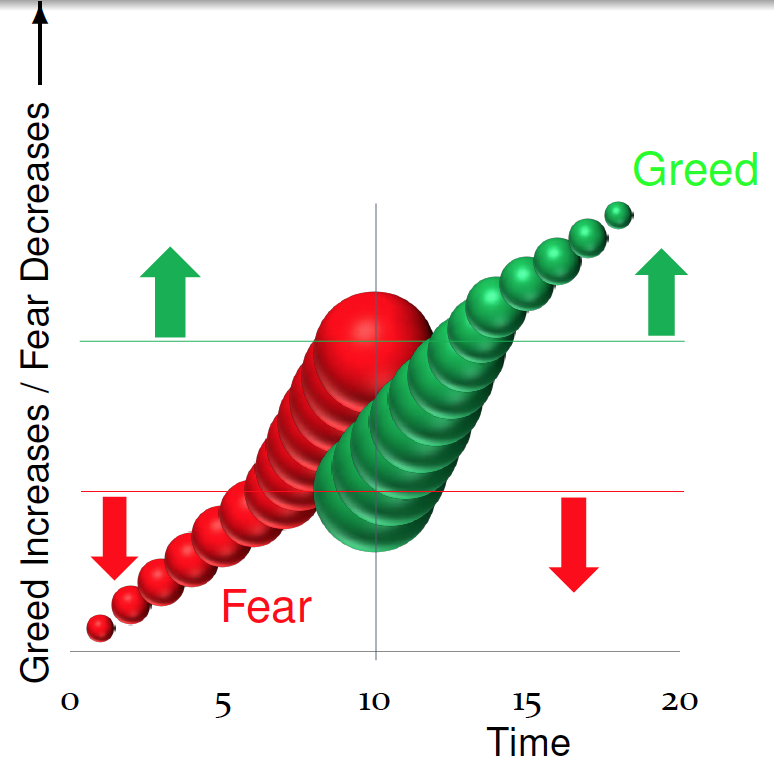
In our paper, fear relaxes the first mover advantage in pre-emption games, asking that the least quantile beat the average; greed relaxes the last mover advantage in wars of attrition, asking just that the last quantile payoff exceed the average. With greed, play is inefficiently late: an accelerating war of attrition starting at optimal time, followed by a rush. With fear, play is inefficiently early: a slowing pre-emption game, ending at the optimal time, preceded by a rush. The theory predicts the length, duration, and intensity of stopping, and the size and timing of rushes, and offers insights for many common timing games:
- Schelling’s Tipping game exploited tatonnement logic on a lattice (mostly). Here, we explain tipping using hump-shaped quantile preferences
- Al Roth has found that sorority and employment matching rushes get earlier and earlier each year; one of his explanations was a tatonnement story, like Schelling We show that these rushes occur long before matching is efficient since they reflect fear. Moreover, the fear increases as the early matching stigma decreases.
- Stock market bubbles often end in a rush. These fit into our rational story of greed, provided there is enough of a reward for mutual fund managers to “beat the average”.
- Bank runs fall into our fear based rushes, and therefore transpire before the efficient time.
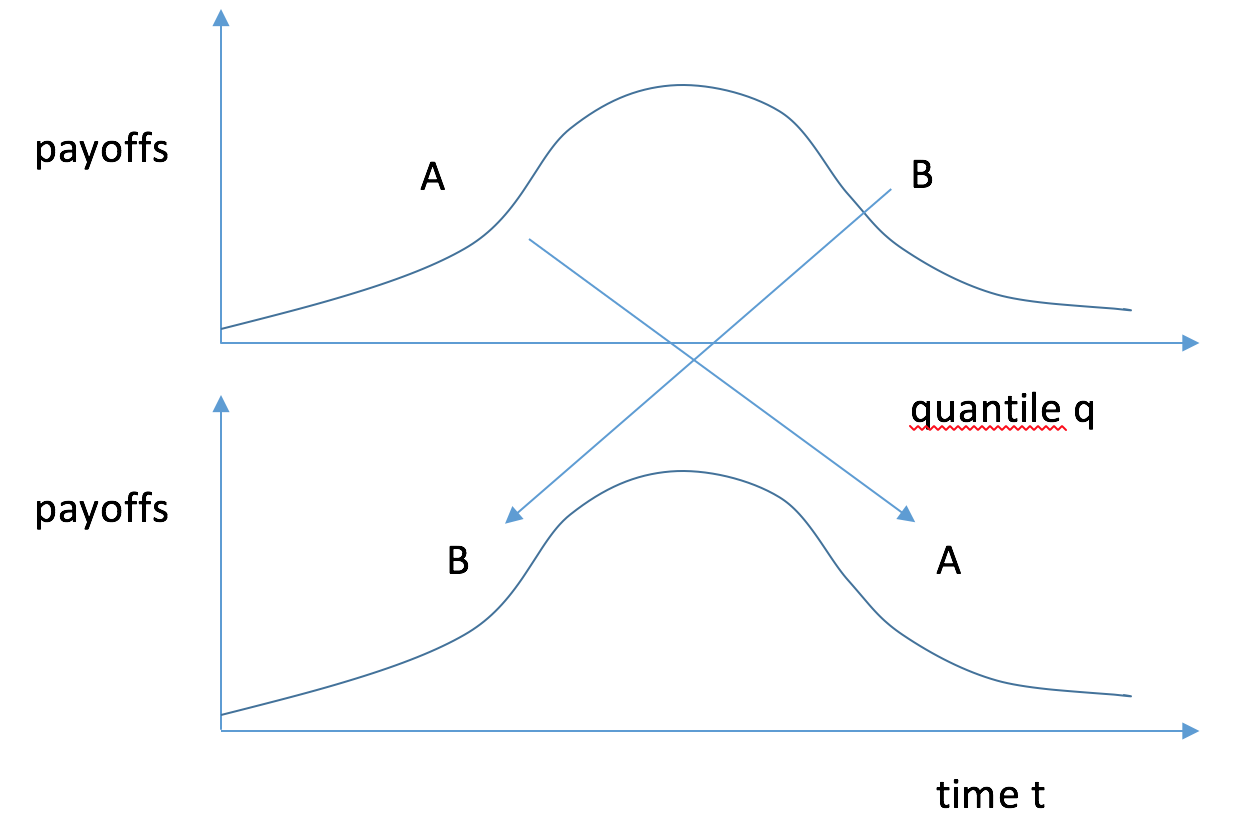
The Simple Economics of Rushes:
Assume that payoffs have the standard “hump shape” as a function of the stopping quantile q, and also separately, as a function of the stopping time t (as in the graph). Assume, towards a contradiction, that there is no rush. Then if people are indifferent about stopping at any time in some intervals, we need at every moment in time (a) payoffs falling in t whenever they are rising in q (our generalization of a pure war of attrition), and (b) payoffs rising in t whenever they are falling in q (our generalization of a preemption game). This is impossible, for then earlier quantile stoppers would have to stop late in time [regions A] and later quantile stoppers would have to stop early in time [region B]. Contradiction
Rushes Occur with Standard Hump-Shaped Payoffs

