“The Comparative Statics of Sorting“, with Axel Anderson (American Economic Review, March 2024)
The transportation problem — the math literature that subsumes the economic problem of optimal pairwise matching — is a famously long unsolved since 1781. Except in very special cases, like supermodularity assumed in Becker, one cannot say who matches with whom in large problems. Yet a long literature since 1990 has shown that Becker’s assumption rules out most applications. So what can you possibly say about this matching problem when you cannot solve it? In our paper, we show how to derive comparative statics on the optimum. To be clear, we derive valid comparative statics even though we have no idea where a matching starts or ends. So our paper iis a case study thus in the advantage of using comparative statics to entirely bypass solving optimizations. Now, how that proof worked even though we had no lattices– that depends on having a coauthor who can work magic with the world’s most clever induction proof.
We create a general and tractable theory of increasing sorting in pairwise matching models with monetary transfers. Our partial order, positive quadrant dependence, subsumes Becker (1973) as the extreme cases with most and least sorting. It implies sorting by correlation of matched partners, or distance between partners.
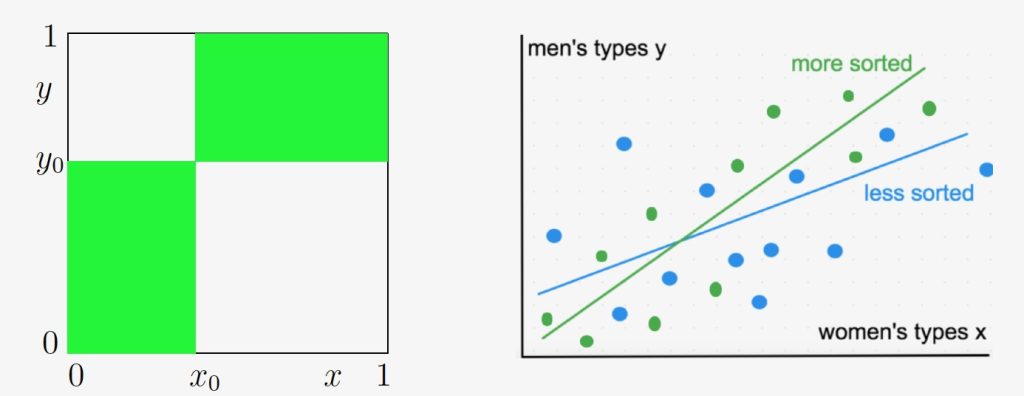
Our theory turns on synergy — the cross partial difference or derivative of match production. This reflects basic economic forces: diminishing returns, technological convexity, insurance, and match learning dynamics. We prove that sorting increases if match synergy globally increases, and is also cross-sectionally monotone or single-crossing. Our theorems shed light on major economics sorting papers, affording immediate proofs and new insights. They open the door to fast predictions for new pairwise sorting models in economics.
We prove that sorting increases if match synergy globally increases, and is also cross-sectionally monotone or single-crossing. Our theorems shed light on major economics sorting papers, affording immediate proofs and new insights. They open the door to fast predictions for new pairwise sorting models in economics.
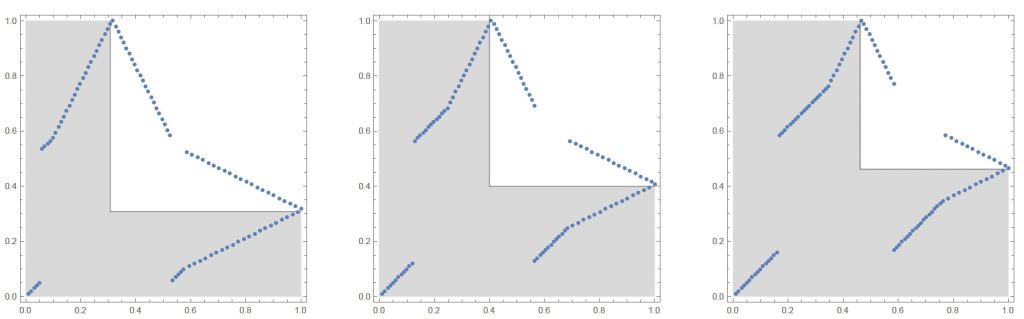
Mathematica Notebooks that Generate Figures in the Paper:
- The README is here.
- For figure 4 the compressed Mathematica file is here.
- For figure 8, the compressed Mathematica file is here.
- For figure 9, the compressed Mathematica file is here.
- For figure 10, the compressed Mathematica file is here.
- For figure 11, the compressed Mathematica file is here.
- For figure 12, the compressed Mathematica file is here.
