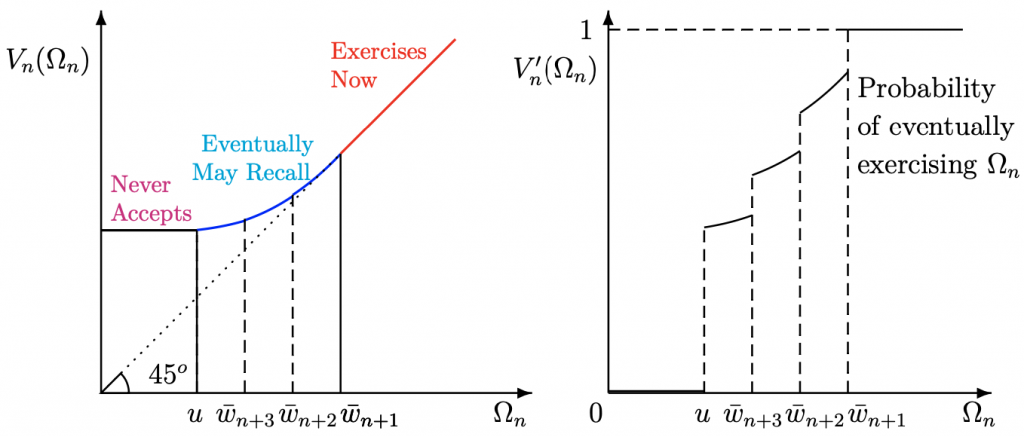
The Economics of Web Search with Michael Choi
We introduce a tractable model of sequential search or choice among distinct pre-ordered options for web search or informed search. We think of this as a general theory of the Pandora’s Box Problem in search: Payoffs are the sum of a random known factor and a random hidden factor, learned after inspection. In this nonstationary search model, prior options are sometimes recalled.
Payoffs are the sum of a random known factor and a random hidden factor, learned after inspection. In this nonstationary search model, prior options are sometimes recalled.
To capture search engines, we assume Gaussian factors, where noise shifts from the hidden to the known factor as web search accuracy rises. The marginal value of web search accuracy is higher eventually than initially. This highlights a possible natural monopoly in web search. Here we see the marginal value of search information as accuracy α rises, where α=1 is the perfect search engine that reads your mind perfectly.
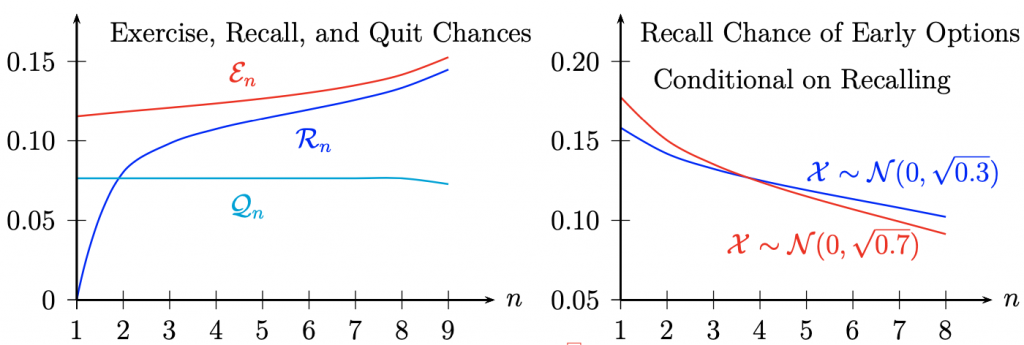
- The search stopping chance rises over time with log-concave factor densities, and the chance of recalling options rises, and older ones are recalled more often
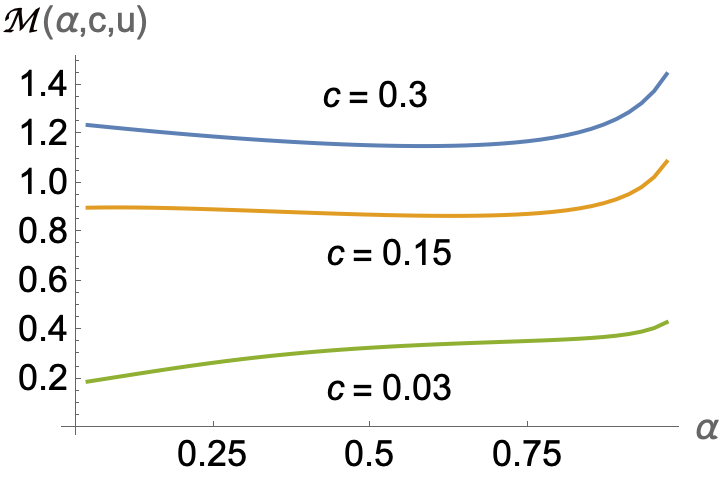
 2. We solve a long open question in all search models: which stochastic changes lead one to search longer? Answer: more dispersed payoffs. Here this means more disperse hidden factors rises. But dispersion of known factors reduces search duration.
2. We solve a long open question in all search models: which stochastic changes lead one to search longer? Answer: more dispersed payoffs. Here this means more disperse hidden factors rises. But dispersion of known factors reduces search duration.
3. The stationary search model poorly approximates search with many options: If the known factor density lacks a thin tail (eg. exponential), the recall chance is boundedly positive with vastly many options.
4. Search lasts longer with more options, since searchers grow more ambitious. Hence, if low search frictions increase worker applicant pools of firms, vacancy duration increases.
