“A Conversational War of Attrition”,  Meyer-ter-Vehn and Smith, and Bognar, Review of Economic Studies (2018)

In juries, tenure cases, FDA panels, Federal Open Market Committee meetings, etc. partially informed individuals share an imprimatur to dispassionately arrive at the truth. Two key features of the meetings are that (1) the search for truth falls short of certainty since the debate is a costly endeavor for all involved, and (2) the debaters might disagree on the costs of different mistaken decisions. This paper develops a simple model of rational debate in which both the length of debate and the wisdom of its decision reflect the debaters’ biases, informativeness, and delay costs.

We explore costly deliberation by two differentially informed and possibly biased jurors: A hawk Lones and a dove Moritz alternately insist on a verdict until one concedes. Their partially aligned preferences give rise to two genres of debate: Lones, say, is intransigent if he wishes to prevail and reach a conviction for any type of Moritz next to concede. In contrast, Lones is ambivalent if he wishes that the strongest conceding types of Moritz would push for acquittal. We show that both jurors are ambivalent if their biases are small, and both are intransigent if waiting costs are low. As Lones grows more hawkish he argues more forcefully for convictions, mitigating wrongful acquittals. If dovish Moritz is intransigent, he softens (strategic substitutes), leading to more wrongful convictions. But if he is ambivalent, he toughens (strategic complements), and so, surprisingly, Lones’ greater hawkishness reduces both wrongful acquittals and convictions.

A key takeout message is that diversity leads to better decisions: more a priori opposed preferences lead to smarter jury decisions. We also show that near the end of the debate, playing devil’s advocate can be optimal if one is patient enough. We shed light on the adversarial legal system, peremptory challenges, and cloture rules.

Our paper develops some useful new theory methods: For equilibria are characterized by a possibly infinite sequence of thresholds obeying a nonlinear second order difference equation. We develop new methods to establish existence and uniqueness. Our existence theorem exploits the Jordan curve theorem as a generalization of the intermediate value theorem. Our uniqueness theorem and comparative statics exploits an assumption that jurors’ information types have a log-concave density.

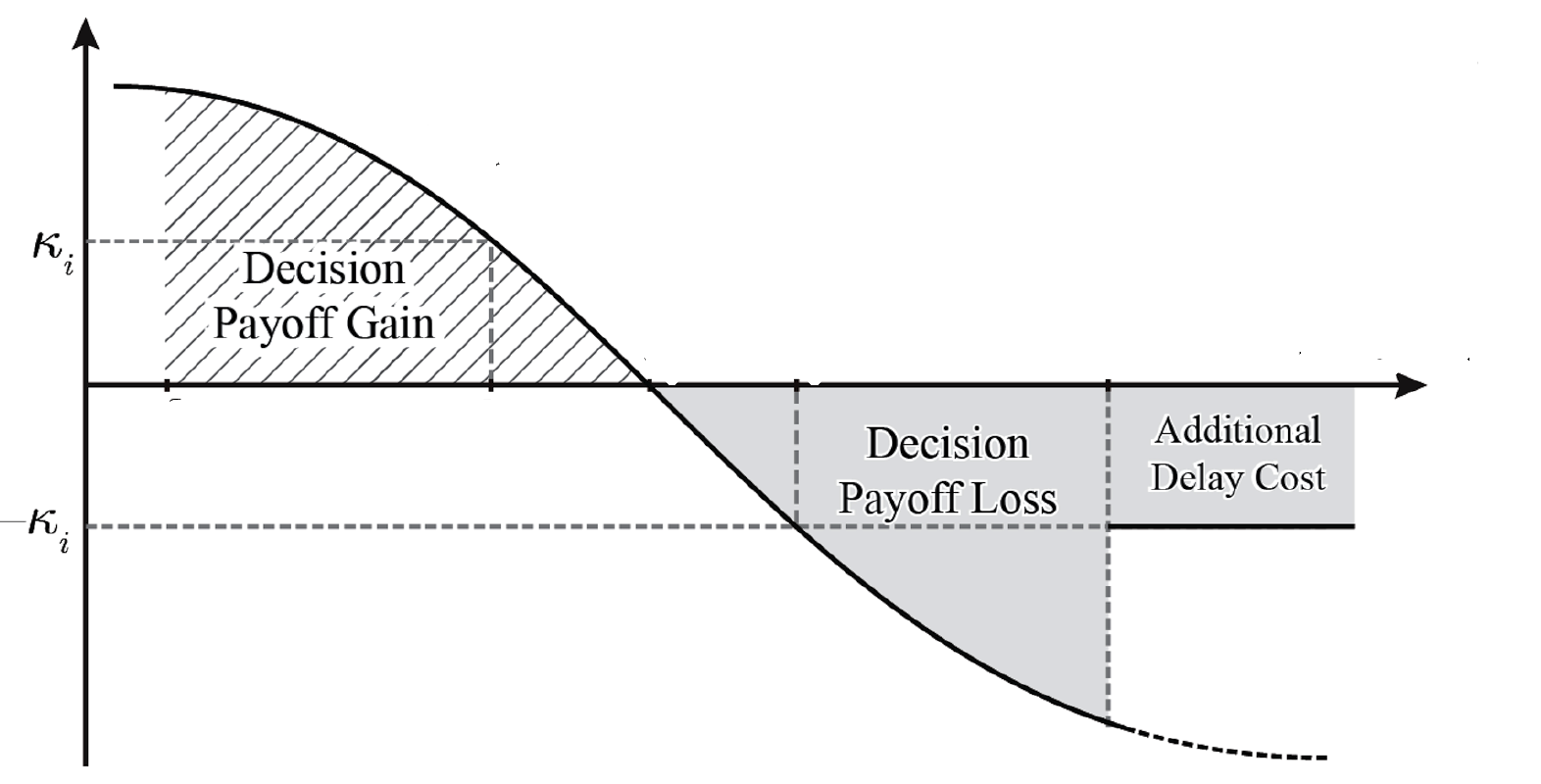
The next picture captures the behavior of a juror as his information grows stronger and stronger on the horizontal axis. As a juror grows more dovish, his cutoff for caving on the debate shifts right. Initially, this encourages the previous juror, and adds to his decision payoff gain. But at some point, the previous juror realizes that by holding out, he has passed the baton to his peer who is far too willing to concede. At this point, we have decision payoff losses. This leads to our fundamental debate taxonomy: that stereotypical intransigent debate never sees jurors worrying about this possibility. Here, debate ends when a juror just “throws in the towel”. But with ambivalent debate, our new discovery, debaters must account for this second decision payoff loss.

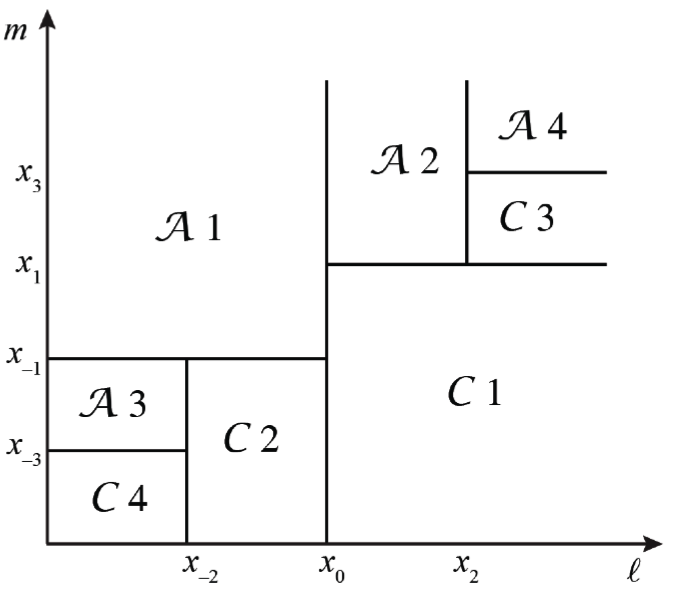
Here we depict how debate ends after period 1, 2, 3, etc with either an acquittal A1 in period 1, or a  conviction C1 later that period, etc.